spotspolt.blogg.se - Advanced sudoku tricks

#ADVANCED SUDOKU TRICKS SERIES#

#ADVANCED SUDOKU TRICKS SERIES#

He is the founder of Grandmaster Puzzles and is the co-author, with Mike Selinker, of the PuzzleCraft series of columns in GAMES magazine. Thomas specializes in hand-crafting artistic, themed logic puzzles, particularly sudoku and variations. Sudoku, is a three-time World Sudoku Champion and six-time US Puzzle Champion. The Art of Sudoku by Thomas Snyder, aka Dr. Recently, many of the top sudoku authors and creators have been publishing theme-based and personalized sudokus, across different variants and some of them are an absolute pleasure to solve. There are lots of books out there for Classic Sudokus. If you did it right, you will be able to logically assume that one of the two wings will be that number.We’ve already covered basic rules and strategies.This is the candidate we can remove from other cells. The two wings will share a pencil mark that the "middle" cell does not have.Found three cells? Great! Now figure out which of the three intersects both the others.Just move on to the next cell and continue. Haven't found any? Most of the time you won't.If you find one, you will have found your "Y". It will need to intersect with one (but not both) of your first two cells. Now it's time to look for a third cell that has the two uncommon pencil marks. For every one you find, you will have a common pencil mark, and two uncommon pencil marks.Scan that cell's block, column, and row for another cell with one of those pencil marks (remember, only look at cells with two pencil marks).For each cell that has two pencil marks, do the following:.

Focus only on the cells that have exactly 2 pencil marks in them ( Sudoklue will highlight these if you press Ctrl-Y).

Start with the top left of the puzzle, working from left to right.

If you are working on a puzzle and find yourself stuck - you can find any more naked pairs, hidden singles, or omissions - maybe it's time to look for an XY Wing: But how could I ever find a situation like this? Well, I'll tell you - it's a bit easier than it may seem… This creates a Lone Single in the right pink cell, solving it. We have, through logic, eliminated 1 as a candidate for the pink cells. Since the green cell dictates that one of the blue cells is going to be "1", we can remove the "1" pencil mark from the pink cells. See two cells colored pink? These two cells intersect both of the blue cells. Let's take a look at the same example again: Now that we know with 100% certainty that one of the wing (blue) cells is a 1, we can assume that any cell that intersects both of the blue cells cannot possibly be a 1! Please read it and study the picture until you are confident you understand it. The previous paragraph is the most important part of this concept. In either case, one of the blue cells is going to be 1. Or perhaps the middle cell is "2"? This would make the left blue cell a 1. Suppose the green cell ended up being "7". The other candidate in each of the wings is the same: a 1.īear with me, I promise I am going somewhere with this! Also notice: one of the wings has a 2, and the other, a 7. In order for this to work, the cell in the middle of the "Y" (green) must intersect both of the cells on its wings (blue), while the two wing cells may not intersect each other.Īdditionally, the green cell's two pencil marks must appear in each of the blue cells' pencil marks, along with a third pencil mark shared by the blue cells only.

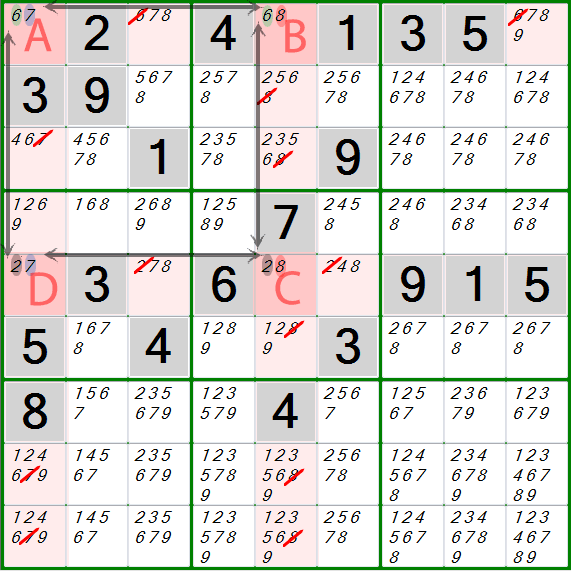
If you ask me, "V Wing" is more appropriate! XY Wing is sometimes just called "Y Wing". The green cell is the middle, and the two blue cells are the "wings". Note how the 3 cells form a "Y" (see the red lines - it's really more like a "V"). XY Wing involves 3 different cells - each with exactly two candidates (pencil marks) - that are related to each other in such a way that you can make some logical conclusions. This of course makes it impossible for them to be the same number. Two cells are said to "intersect" if they share a row, column, or block. In order to follow what is explained below, it is important to first understand the concept of Intersection. But I have devised a method for finding them, and I will pass it on to you a bit later in this page. That having been said, XY-Wing is not easy to find. It's one of those things where, after a little time, I finally came to understand how and why it works, but deep down inside I know I could have never thought it up on my own. I guess it's because the logic is just so perfect!